e sayısı
e sayısı, matematikte iki tam sayının bölümü şeklinde yazılamayan, yani rasyonel olmayan bir sayıdır. Değeri yaklaşık olarak 2,718281828459... civarındadır. Leonhard Euler, Introductio it analysin infinitorum isimli 1748 tarihli eserinde bu sayıdan bahsettiği için buna Euler sayısı da denir. Matematiksel ifadelerde çok karşılaşılması yönünden bu sayı önemlidir. Tabiatta pek çok faaliyet aşağıdaki karekteristiğe sahiptir. Herhangi bir büyüklüğün miktarında meydana gelen değişiklik büyüklüğün miktarına bağlıdır. Bu, bir tabaktaki bakteri, radyoaktif madde miktarı veya elektrik akım miktarı olabilir. Her durumda da olayın gelişimi (k) değişim miktarını gösteren bir sabit olmak üzere dy/dt=ky şeklinde matematiksel olarak temsil edilir. Bu denklemin çözümü y=A·ekt şeklindedir. Burada A başlangıç şartlarına bağlı bir katsayıdır. Bu ifade y=A·exp (kt) olarak da yazılabilir ve bu tür ifade, k'nin pozitif veya negatif olmamasına bağlı olarak kuvvet (eksponansiyel) artma veya azalma olarak isimlendirilir. e veya exp (kt) olarak yazılan üstel (eksponansiyel), fonksiyon kimyanın pekçok dalında ortaya çıkar. e'nin kuvvetleri ve e'i taban alan logaritma (tabii logaritma) değerleri tablolaştırılarak kolay kullanılır duruma sokulmuştur. e sayısının rastlanmasına pratik bir misal olarak bir lira % 10 faiz altında bir yıl sonra iki lira olur. Ancak faizler altı aylık hesaplanırsa bir yıl sonra 2,25 lira olarak ortaya çıkar. Eğer faiz üç aylık hesaplanır ise bu sonuç 2,37 civarındadır. Ancak faiz hesaplama süresi azaldıkça sonuç e=2,718... değerine yaklaşır.
Euler sayısının diğer bir tarifi de
- limit olarak
 -
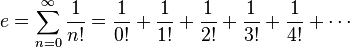 dır. dır.
-
-
Karmaşık (kompleks) sayılar da:
e^iQ = cos Q + i sin Q olarak ifade edilir.

yazılan ve rasyonel olmayan e ile i arasındaki ilişkiyi de Euler göstermiştir.
1 + (1/1!) + (1/2!) + (1/3!) + (1/4!) + ... + (1/n!) serisinin toplamı da
"e" sayısını verir.
Yaklaşık değeri:
e=2.71828182845904523536028747135266249775724709369995957496
6967627724076630353547594571382178525166427427466391932003....
dir. |